# How it Works

The Bitcoin Computer protocol associates JavaScript values with the outputs of Bitcoin transactions that contain JavaScript expressions.

# Storing Values

To compute the value associated with an output, the expression is first evaluated. If the expression evaluates to a basic type, this value is associated with the first output. If the value is nested and contains multiple sub-objects, each sub-object is associated with a separate output.

This simple mechanism makes it possible to store arbitrarily complex Javascript values in the outputs of a transaction using an highly efficient encoding: Instead of storing a value, an expression is stored that computes the value. This is much more efficient. In fact, it makes it possible to store a value at its optimal compression (see the Kologromov Complexity).

# Example

Consider a transaction that contains the JavasScript expression '0'.repeat(100000). In this case the first output of the transaction is associated with a string of 100,000 zeroes.

Note that this encodes a 100,000 character string in just 18 characters

# Updating Values

Expressions can contain undefined variables. For example, the variable x is undefined in the expression x+4. It is not possible to evaluate an expression with an undefined variable. For example, an Javascript interpreter will throw a ReferenceError when trying to evaluate x+4.

In the Bitcoin Computer protocol, expressions with undefined variables are used to encode data updates. To determine a value for the undefined variables, the undefined variables in an expression must be associated with inputs of the transaction. The protocol will then compute the values associated with the outputs spent. These values are the substituted (aka plugged into) the respective undefined variables. This yields an expression where all variables are defined that can be evaluated. The value returned from this evaluation is associated with the outputs as explained in the previous section.

# Example

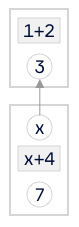
Consider the transactions on the left. The first is labelled with 1+2. This expression contains no undefined variables and evaluates to 3, therefore the output of the first transaction is associated with the value 3.

The expression x+4 on the second transaction contains the undefined variable x. The input of this transaction is associated with this undefined variable. To compute the value associated with the output of the second transaction, the Bitcoin Computer protocol first computed the value of the output spent, which is 3. This value is then substituted for x in the expression x+4. This yields the expression 3+4 which evaluates to 7. This is the value associated with the output of the second transaction.

# The Interface

We call a string of the form id:num where id is a transaction if and num is an output number a revision. The following two functions provide access to the protocol through two main functions:

• sync maps a revision to a value.
• encode maps an expression and a blockchain environment to a transaction.

# Provenance

If the value returned from sync contains an object, it has extra properties _id, _rev, _root that specify its location on the blockchain and its provenance.

• The identity of an object, denoted obj._id, is a unique identifier that remains unchanged throughout the object's lifecycle. It is set to the transaction and output that the object was associated to when it was first created.
• The revision of an object, denoted obj._rev, encodes an object's current location on the blockchain.
• The root of an object, denoted obj._root, records whether obj was created in a function call of another object, and if so which object that was.

# Keyword Properties

Smart contracts can contain the keyword properties _owners, _amount, _url and _readers that determine how the transaction is built. Specifically

• The _owners property of a smart object determines the output script of the output that is associated with it. If it is set to an array of strings that encode public keys, then the output script will be a 1-of-n multisig script with these public keys. If it is set to a string that encodes a Bitcoin Script ASM, then that will be the script of the output.
• The _amount property can be set to a number and determined the amount of satoshi of the output associated with a smart object. If this property is undefined the output will contain a minimal, non-dust amount of satoshis.
• The _url property can be set to the url of a Bitcoin Computer node. If set the metadata that would otherwise be stored in the transaction is stored on that node. The metadata will consist only of a url where the data can be obtained.
• The _readers property can be set to encrypt the meta data. It can be set to an array of strings encoding public keys. In this case the metadata on the transaction will be encrypted such that only the specified users can decrypt the data and read the object.